Ponoć matematyka jest królową nauk i wygląda na to, że tym tytułem zaraz okrzyczą ją marynarze. Określono bowiem model matematyczny, który przewiduje stabilność węzłów.
Matematycy i inżynierowie z MIT wykorzystali włókna zmieniające kolor, aby umożliwić to odkrycie. Dokonali tego prosto, łącząc podejście teoretyczne ze znacznie praktycznym, dzięki czemu opracowany model może wyjaśnić, dlaczego jeden węzeł jest lepszy do konkretnego zastosowania niż inny.
Rolę węzłów oraz ich rozwoju na przestrzeni lat wystarczy zaakcentować tym, że pełniły ważną funkcję już u starożytnych greckich żeglarzy. Dotąd są używane na co dzień do wiązania butów, owijania paczek, zabezpieczania drutów, plecenia sieci, czy tworzenia prostych dekoracji.
Najgorsze jest jednak to, że nadal ich nie rozumiemy. To tysiące prób i błędów zaowocowało solidną wiedzą praktyczną na temat tego, które węzły są najlepsze do jakich zadań, ale niewiele pozostawało w tym teorii. Przynajmniej do tej pory.
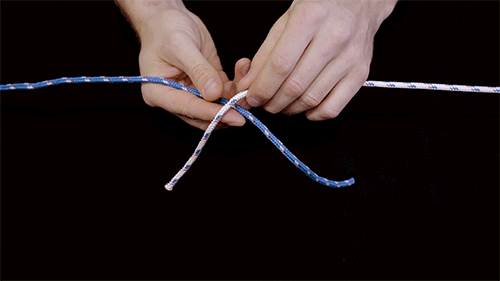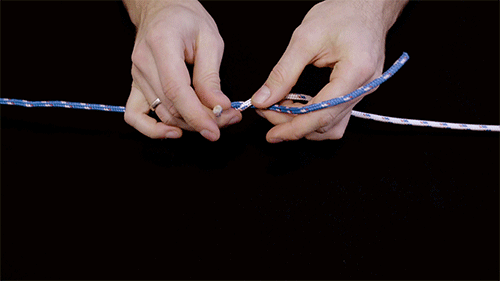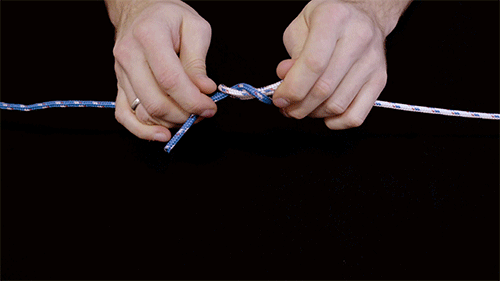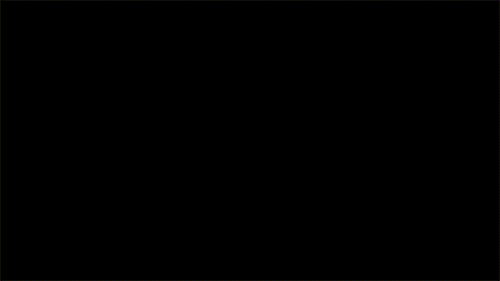
Węzły z naukowego punktu widzenia uznano bowiem za gałąź topologii matematycznej, gdzie podchodzi się do nich za pomocą wzorców teoretycznych. Jak tłumaczy Jörn Dunkel, profesor matematyki w MIT:
W matematycznej teorii węzłów porzucaszwszystko, co jest związane z mechaniką. Nie obchodzi cię, czy masz sztywne i miękkie włókno – to ten sam węzeł z punktu widzenia matematyka.
Chcieliśmy jednak sprawdzić, czy moglibyśmy dodać coś do matematycznego modelowania węzłów, które uwzględnia ich właściwości mechaniczne, aby móc powiedzieć, dlaczego jeden węzeł jest silniejszy od drugiego.
W rzeczywistości dwa węzły, które wyglądają bardzo podobnie do siebie, mogą mieć bardzo różne właściwości. Właśnie dlatego zespół MIT zwrócił się do modeli matematycznych.

Opracowany przez nich model opierał się na zachowaniu włókien, ale z tym wyjątkiem, że nici zostały zastąpione w symulacji małymi, dyskretnymi, połączonymi sprężyną kulkami, aby ułatwić liczenie oddziałujących na nie sił. Ponadto zastosowane włókna zmieniały kolor z jednego odcienia na drugi w odpowiedzi na naprężenia, zapewniając wizualne wskazówki, jak zachowuje się węzeł.
Wykorzystując włókna do tworzenia różnych węzłów i fotografując wyniki, Dunkel i Kolle byli w stanie zgromadzić rzeczywiste dane, które można było wprowadzić do modelu. To pozwoliło uporządkować węzły według ich siły i stabilności.
Wnioski? Im więcej razy węzeł się krzyżuje i im bardziej zmienia się kierunek obrotu, tym staje się on stabilniejszy.