Wszystko zaczęło się około 250 roku przed naszą erą, kiedy to Diokles napisał książkę Burning Mirrors, rozprawiającą o aberracji sferycznej. Zjawisku, które nęka fotografię od momentu jej powstania i objawia się miękkimi krawędziami bez względu na to, jak wysokiej jakości jest aparat. Matematyki bowiem nigdy nie oszukamy, a ta jasno wskazuje, że krzywa soczewek optycznych zawsze będzie nieco bardziej miękka niż środek.
Czytaj też: Teleskop ALMA bada „strefę wpływów” czarnej dziury
Jednak ten problem rozwiązał Rafael G. González-Acuña (we współpracy z Gonzálezem Acuñą), doktorant w meksykańskim Tecnológico de Monterrey, który może i działania matematyki nie zmienił, ale opracował sposób, w jaki aberracja sferyczna przestała mieć większe znaczenie.
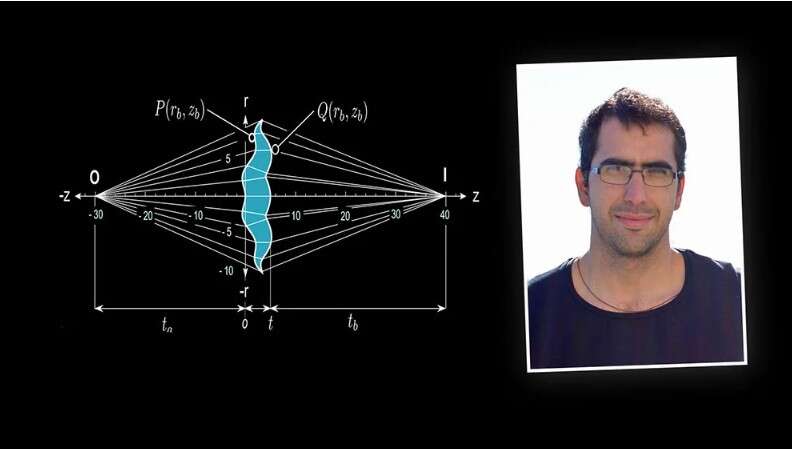
Warto najpierw wyjaśnić to zjawisko w uproszczony, fizyczny sposób. Polega ono na tym, że gdy promienie światła padają na soczewkę, różne promienie nie spotykają się za soczewką w jednym punkcie ogniskowym. Wszystko przez niedoskonałości obiektywu, które uniemożliwiają całkowite wyeliminowanie wspomnianego zjawiska.
I tak też stoimy tutaj po grubo ponad 2000 lat od pierwszego nakreślenia pojęcia aberracji sferycznej i w czasach, w których jej problem został rozwiązany przez doktoranta na UNAM. Oczywiście z wykorzystaniem matematyki i to w wydaniu, które strąca sen z powiek każdego studenta. Wygląda ono bowiem tak:
Sam naukowiec opisuje je następująco:
W tym równaniu opisujemy, jak kształtowi drugiej powierzchni asferycznej danej soczewki należy nadać pierwszą powierzchnię, którą zapewnia użytkownik, a także odległość obiektu od obrazu. Druga powierzchnia jest taka, że koryguje całą aberrację generowaną przez pierwszą powierzchnię, a aberracja sferyczna jest eliminowana.
To odkrycie może sprawić, że sprzęt naukowy, medyczny i wreszcie konsumencki przeżyje w następnych latach rewolucję.
Czytaj też: Czarnobylski sarkofag zostanie zdemontowany
Źródło: Popular Mechanics